활성화 함수(Activation Function)

1. 활성화 함수란?

신경망의 특징 중 하나인 활성화 함수는 신경망 층의 선형 방정식의 계산 값에 적용하는 함수입니다. 활성화 함수는 비선형 문제를 해결하는데 중요한 역할을 합니다. 인공신경망에서 활성화 함수는 입력 데이터를 통해 다음 레이어로의 출력에 중요한 역할을 합니다. 즉, 활성화 함수는 입력을 받아 활성화 또는 비활성화를 결정하는데 사용되는 함수입니다. 활성화 함수는 주로 비선형 함수를 사용합니다. 선형함수같은 경우는 층을 깊게 하는 의미가 줄어들기 때문에 반드시 비선형 함수를 사용해 줘야합니다.

예를 들어 선형함수인 $h(x) = ax$를 활성화 함수로 사용하고 3개층이 있다고 가정을 합니다. 그러면 해당 층을 식으로 나타내면 $y(x) = h(h(h(x)))$이 되면 결국 $h(x) = a^3x$과 같은 식이 나오기 때문에 수십개 쌓여도 하나의 linear 연산이 나오게 됩니다. 결국 활성화 함수는 비선형 함수를 사용해줘야 합니다.

---

2. 활성화 함수 종류

2 - 1. 계단함수 (Step function)

계단함수는 이진 분류를 나타내는 함수로 1아니면 0을 출력해줍니다. 장점으로는 0과 1만을 출력해주기 때문에 단순한 구조로 이루어져 있지만 다중 출력이 불가능하고 합산된 값이 0.1이든 1.0이든 모두 무시하고 1로 전달하므로 출력되기 때문에 결과값이 아쉬운 평가를 가지고 있습니다. 계단 함수는 퍼셉트론에서 쓰이고 있습니다.

2 - 2. 시그모이드 함수

시그모이드 함수는 S자형 곡선 또는 시그모이드 곡선을 갖는 함수입니다. 이 함수는 임의의 실수 값을 입력으로 받아 0에서 1 사이의 값을 출력합니다.

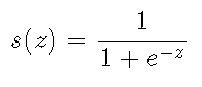
아래 그림과 같이 입력 값이 클수록 출력 값이 1에 가까워지고 입력이 작을수록 출력이 0에 가까워지는 함수입니다.

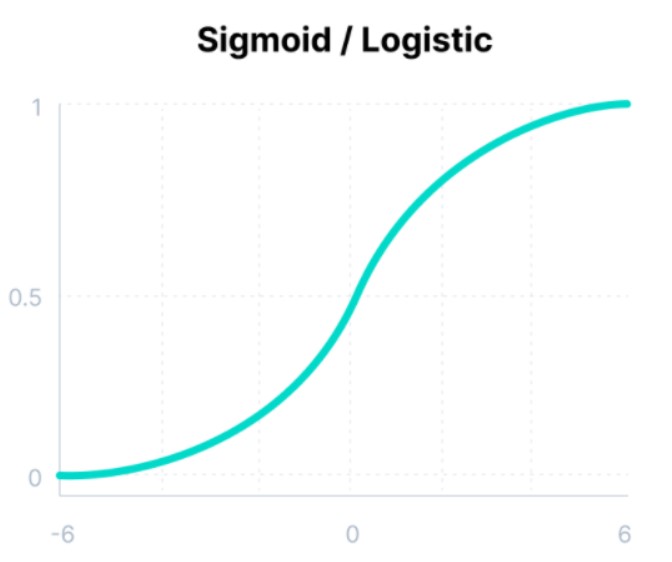
시그모이드함수는 범위가 0 ~ 1사이에만 존재하므로 확률을 출력으로 예측해야 하는 모델에 사용됩니다. 시그모이드 함수는 출력값의 범위가 0 ~1로 제한하기에 정규화 관점에서 exploding gradient(기울기 폭주) 문제를 방지할 수 있습니다.

Vanishing gradient(기울기 소실)은 입력층으로 갈수록 기울기가 점차적으로 작아지는 현상이 발생할 수 있습니다. 입력층에 가까운 층들에서 가중치들이 업데이트가 제대로 되지 않으면 최적의 모델을 찾을 수 없습니다. 이러한 것을 기울기 소실이라고 합니다. 반대로는 기울기가 점차 커지면서 가중치들이 비정상적으로 큰 값이 되면서 발산이 되는 것을 exploding gradient(기울기 폭주)라고 합니다.

하지만 시그모이드 함수에 단점이 있어 최근에는 잘 사용되지 않는다고 합니다. 바로 위에서 설명한 Vanishing gradient(기울기 소실) 문제를 갖습니다. 시그모이드 함수는 음수 값을 0에 가깝게 표현하기 때문에 입력 값이 최종 레이어에서 미치는 영향이 적어지기 때문입니다.

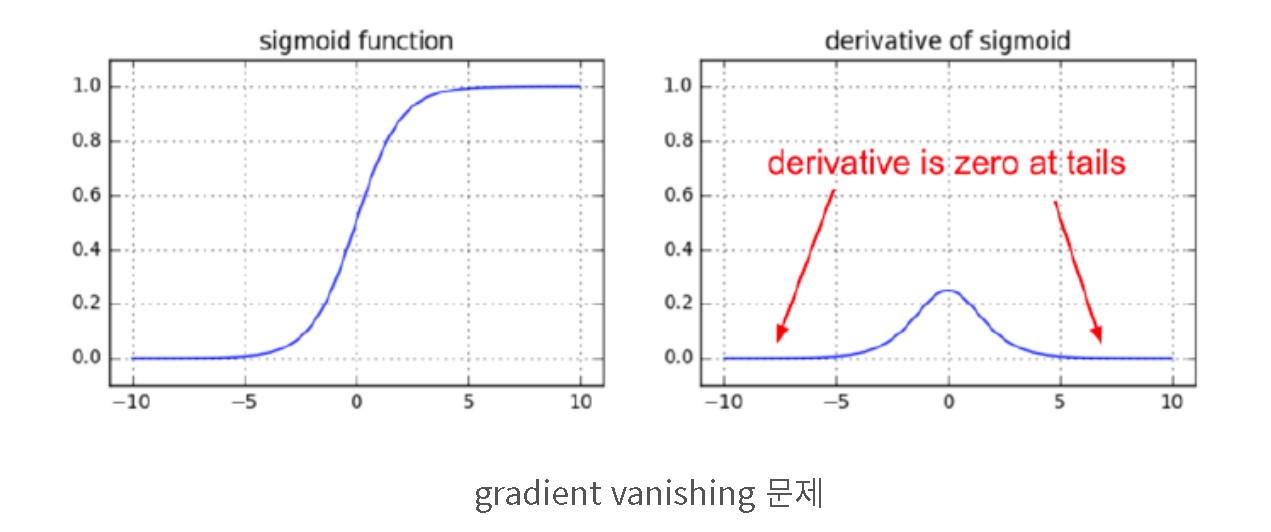
시그모이드 함수의 도함수를 구해보면 $x = 0$에서 최대값 0.25를 갖는다. 입력값이 작거나 커질수록 기울기는 0에 수렴하게 되면서 가중치가 갱신이 되지 않습니다. 즉 은닉층의 깊이가 깊으면 오차율을 계산하기 어려워 Vanishing gradient(기울기 손실)이 발생합니다. 학습의 효율이 매우 떨어져 최근에 잘 사용되지 않고 있습니다.

2 - 3. 렐루함수

딥러닝에서 가장 많이 사용되는 활성화 함수중에 렐루함수도 있다. 렐루 함수는 층이 많은 심층 신경망일수록 효과가 미비해지는 시그모이드와 같은 함수를 개선하기 위해 만들어진 함수입니다. 렐루함수는 간단하게 입력이 양수일 경우 마치 활성화 함수가 없는 것처럼 입력을 통과시키고 음수일 경우에는 0으로 만들어 줍니다.

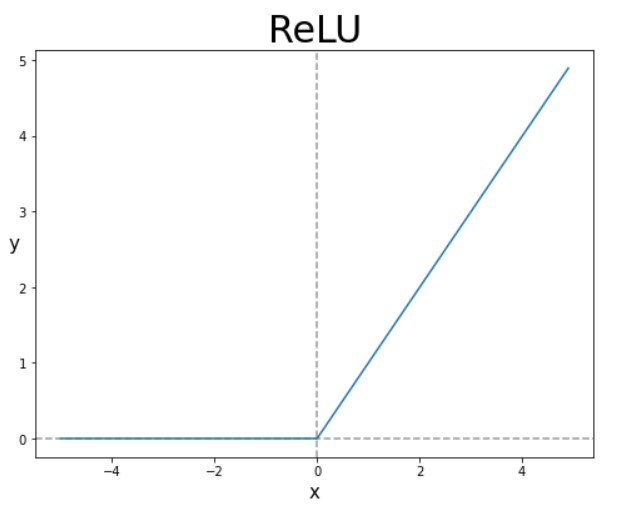
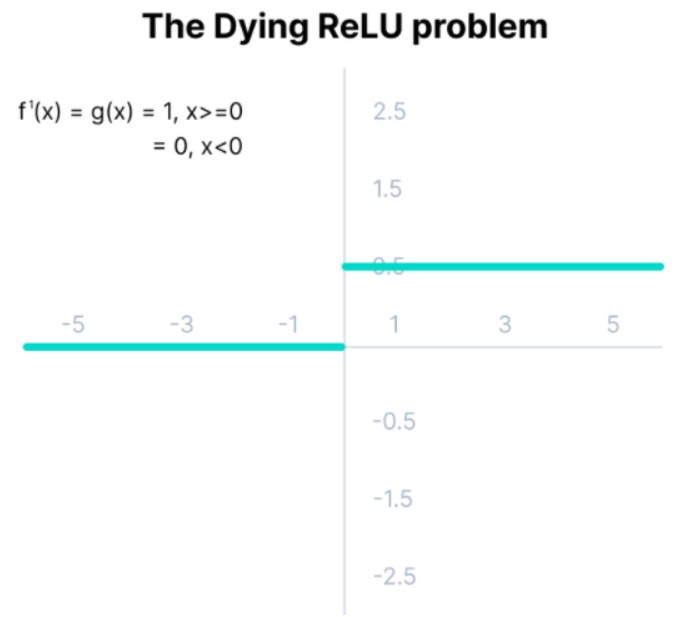
렐루 함수를 은닉층에서 많이 사용하는 이유로는 기울기 소실 문제가 발생하지 않습니다. 렐루 함수는 양수는 통과시키고 음수일 경우 0으로 만들어주기 때문에 특정 양수 값에 수렴하지 않습니다. 출력값의 범위가 넓고, 양수인 경우 자기 자신을 그대로 반환해주기 때문에 시그모이드 함수의 문제인 기울기 손실이 발생하지 않습니다. 또한 단순한 공식이다 보니 학습속도가 빠르다는 장점이 있습니다. 확률적 경사하강법(SGD)을 쓸 때 시그모이드 함수에 비해 수렴속도가 약 6배 정도 빠릅니다. 하지만 이런 렐루 함수의 단점도 존재하는데 먼저 입력값이 음수인 경우 모두다 0으로 반환된다는 문제가 있습니다. 이러한 문제는 데이터를 적절하게 맞추거나 훈련하는 모델의 기능이 감소합니다. 이러한 이유는 가중치가 업데이트 되는 과정에서 가중치 합이 음수가 되는 순간 ReLU는 0을 반환하기 때문에 뉴런은 0만 반환하는 아무것도 변하지 않은 현상이 발생합니다. 이러한 현상을 죽어가는 뉴런(Dying ReLU)현상이라고 합니다. 다음에는 Dying ReLU에 대해 다뤄보겠습니다.