지니 불순도와 엔트로피 불순도
1. 지니 불순도(Gini impurity)란?
지니불순도라는 것은 데이터 분석에서 흔히 의사결정나무에서 사용되는 클래스개수에 따른 케이스들의 불순한 정도를 나타내는 척도라고 생각하면 된다. 불순도는 다양한 범주들의 개체들이 얼마나 포함되어 있는지를 의미한다. 즉 여러 가지의 클래스가 섞여 있는 정도를 말한다. 순수도는 이와 반대로 같은 클래스끼리 얼마나 많이 포함이 되어 있는지를 말한다.
예를 들어, 아래와 같이 항아리가 3개가 있다고 가정하자. 1번 항아리와 2번 항아리는 순도가 100%라 할 수 있고 2번 항아리는 불순도가 높은 상태라 할 수 있습니다. 아래와 같이 항아리 3개가 있을 때, 1번과 3번 항아리는 순도 100%라 할 수 있으며, 2번 항아리는 불순도가 높은 상태라 할 수 있다.
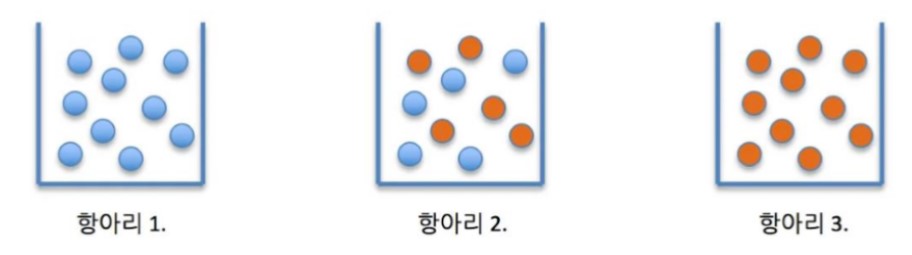
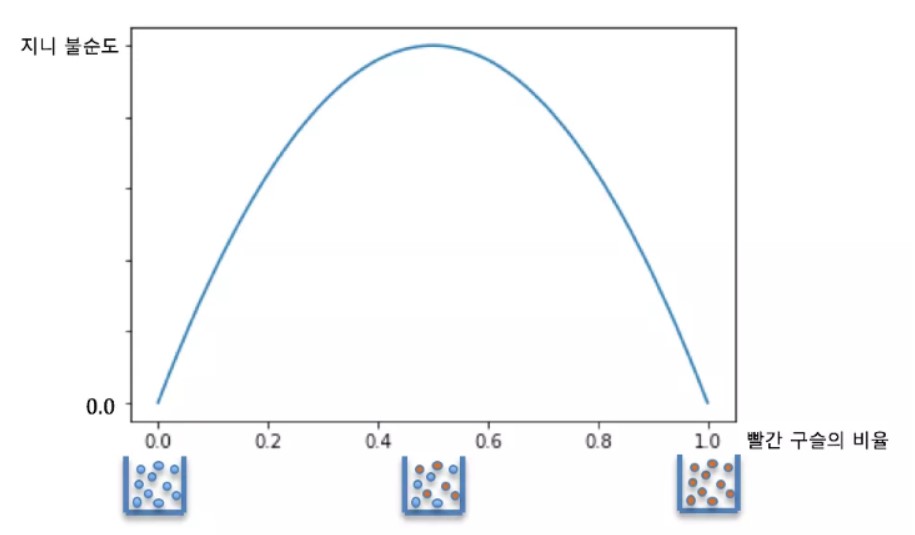
그래프로 다시 불순도를 나타내면 아래와 같은 그래프를 만들 수 있다. 양쪽 끝은 순수한 항아리로서(항이리1과 항아리3) 지니 불순도 0이다. 2번의 항아리같은 경우 빨간색 및 파란색 구슬의 수가 같은 경우 지니 불순도는 최댓값을 갖는다. 불순물없이 깨끗하게 분류가 되어 있으면 0값을 가지지만 섞이게 되면 0보다 큰 값을 가지게 되고 최댓값은 0.5를 가지게 된다.
이를 수학적 식으로 나타내면 이러한 식을 얻을 수 있다.
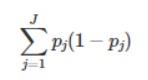
예를 들어 구슬 10개 중에서 파란구슬이 4개가 빨간 구슬이 6개가 있다면 지니불순도는 아래와 같이 구할 수 있다.
\(1 - ((4/10)^2 + (6/10)^2) = 0.48\)
48% 정도의 불순도를 나타낸다.
2. 정보이득(Information Gain)란?
지니 불순도를 구할 수 있다면, 이를 통해 정보 이득(Information Gain)을 계산할 수 있다. 부모노드와 자식노드 사이의 불순도 차이를 정보 이득이라고 부릅니다. 정보량이 작을수록 순도가 더 높기 때문에 확률도 더 높습니다. 따라서 자식 노드로 나눠질 때 정보량이 가장 작아지는 것이 좋습니다. 즉 Gain(A) 값이 클수록 정보 이득이 큰 것이고, 변별력이 좋다는 것을 의미한다. 변별력이 좋다는 것은 분류가 더 잘 되었다는 뜻입니다.
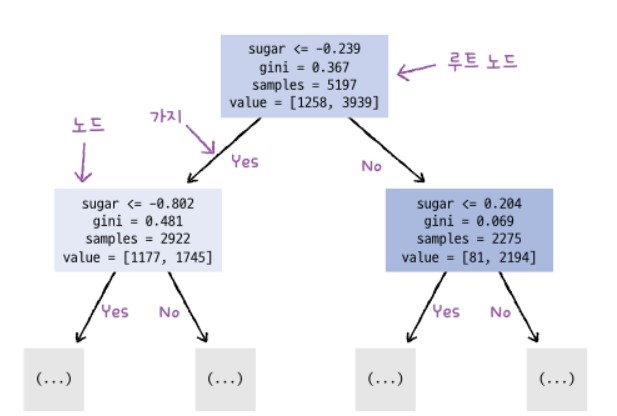
위의 그래프를 보면 아래와 같은 식을 얻을 수 있습니다.

3. 엔트로피(Entropy)란?
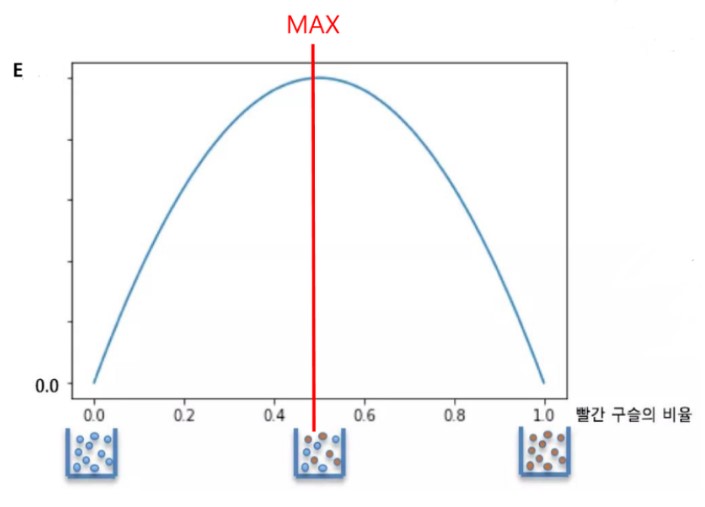
엔트로피는 데이터의 분포의 순수도(purity)를 나타내는 척도이며, 어떤 집합의 무질서 정도를 측정하는 수치이다. 범위는 0부터 1까지로 나타낸다. 엔트로피가 0이면 완전 순수하며 1이면 완전 불순하다는 것을 의미한다. 즉, 데이터의 순도가 높을 수록 엔트로피의 값은 낮아지고, 많이 섞이면 섞일수록 엔트로피의 값이 커지게 된다.
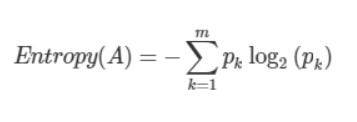
항아리 순도가 100% 일 때에는 엔트로피는 0이다. 하지만 두 구슬 반반 섞여 있을 때에는 엔트로피는 최대값을 갖는다. 즉, 데이터의 순도가 높을 수록 엔트로피의 값은 낮아지고, 많이 섞이면 섞일수록 엔트로피의 값이 커지게 된다.
엔트로피 불순도를 사용할 경우 제곱이 아닌 밑이 2인 로그를 사용하여 곱합니다.
4. 지니와 엔트로피의 차이
지니 불순도와 엔트로피 불순도는 많은 차이가 나지 않습니다. 보통의 경우는 지니보다 엔트로피가 더 나은 성능을 나타내긴 합니다. 그래프로 그려보면 지니 그래프가 엔트로프 그래프보다 경사가 더 급한 것을 볼 수 있어 엔트로피가 모델을 더 잘 분류한다고 봅니다. 하지만 지니가 엔트로피보다 연산 속도는 더 빠릅니다. 엔트로피는 로그를 사용하기 때문에 속도의 차이가 나 데이터가 증가할수록 지니가 연산 속도가 더 빨라집니다. 지니는 빠른 계산을 원할 때, 엔트로피는 시간을 더 투자하더라도 지니보다 확실한 성능을 얻고자 할 때 사용합니다. 지니와 엔트로피는 각각의 장단점이 있어 원하는 값을 얻을 때 적절한 방법을 택해야 합니다.

댓글남기기