선형회귀 쉽게 이해하기

1. 선형회귀란?

어떤 변수의 값에 따라서 x값이 증가하거나 감소할 때 y값 또한 증가하거나 감소하는 하는 경우 독립 변수가 1개라면 단순 선형 회귀라고 합니다.

• 키가 클수록 몸무게가 증가한다.
• 공부를 많이 할수록 시험점수가 오른다.

이와 같이 독립변수는 여러개가 될 수 있고 종속 변수는 하나만 올 수 있습니다. 선형 회귀는 한 개 이상의 독립 변수 와 의 선형 관계를 모델링합니다. 만약, 독립 변수 가 1개라면 단순 선형 회귀라고 합니다.

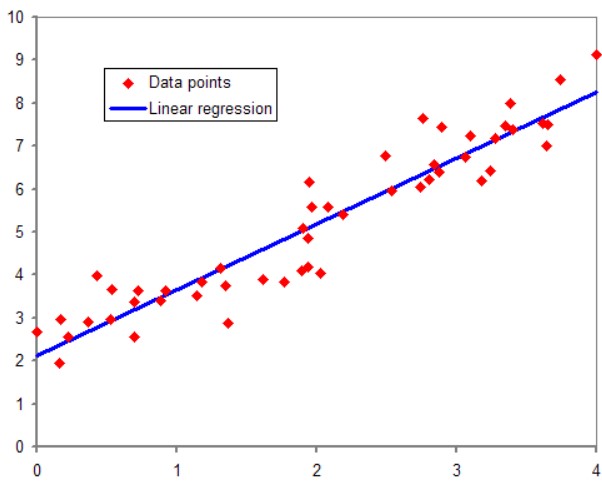
그렇다면 예상값이 정확히 일치하냐?하고 물으면 일치하지는 않습니다. 이는 근사치로 정확하지는 않고 최대한 가깝게 추정할 수 있도록 도와줍니다.

$h(x)=θx+z$

기울기 θ, 절편 z에 따라 그 선의 모양이 정해지기 때문에 x를 넣었을 때 y를 구할 수 있습니다. 우리가 찾고자 하는 목적은 선형회귀분석을 가장 잘 나타내는 θ와 z를 찾는 것입니다. 머신러닝에서 기울기는 가중치라고 부릅니다.

---

2. 선형회귀에서의 오차, 손실

우리는 선형회귀에서 정확한 값을 찾을 수 없고 근사값을 찾을 수 있습니다. 이와 같이 정확한 값과의 차이를 우리는 오차, 머신러닝에서는 손실이라고 부릅니다.

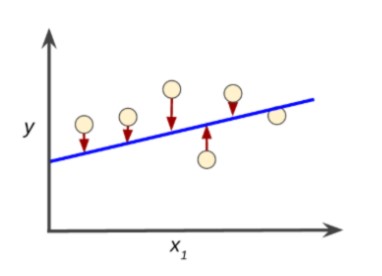
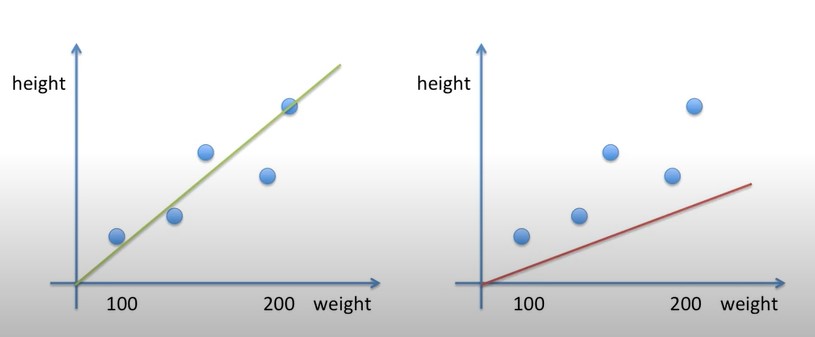
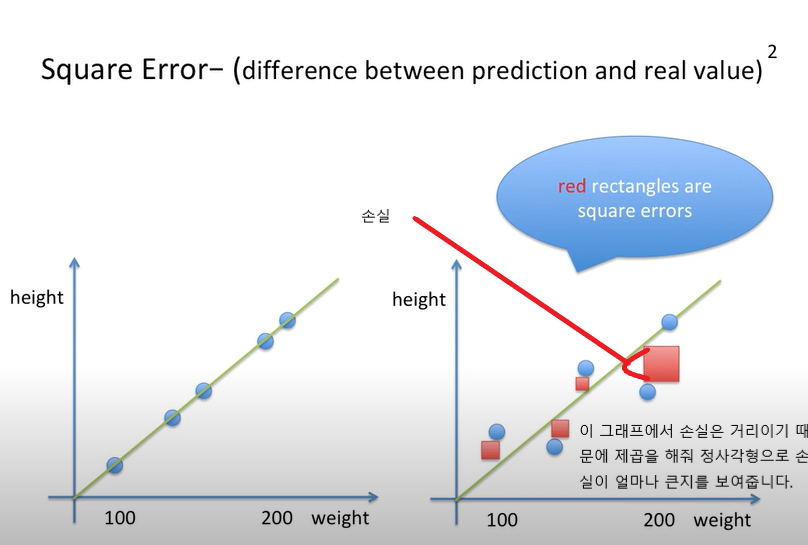
손실의 값은 음수가 될 수도 있고 양수가 될 수도 있습니다. 우리는 실제 데이터와 선과의 손실이 얼마나 차이가 있는지 알아보기 위해 손실을 제곱 해줍니다. 제곱을 해주는 이유는 손실이 얼마나 큰지를 보여주기 위함입니다. 이런 방식으로 손실을 구하는 걸 평균 제곱 오차(mean squared error, 이하 MSE)라고 부릅니다.

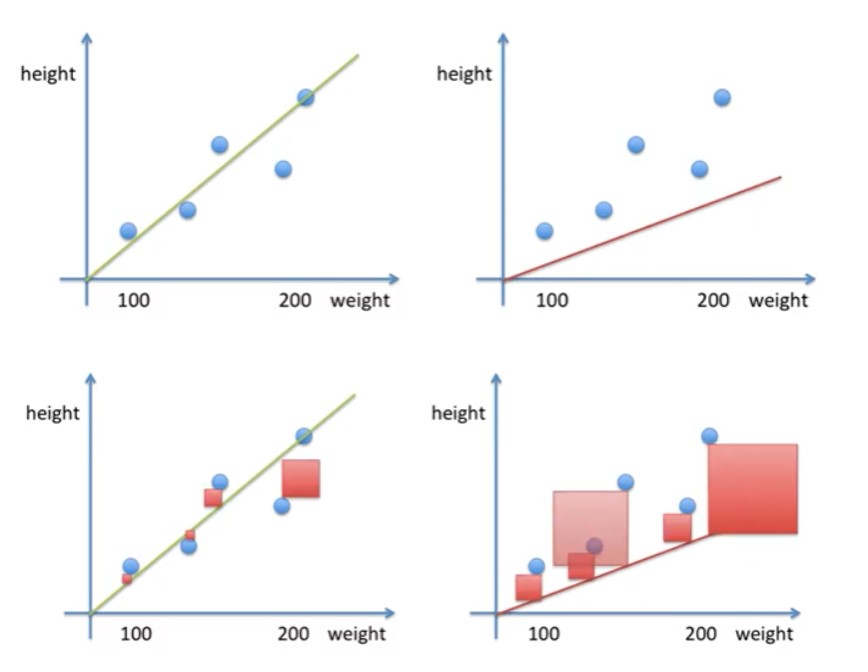
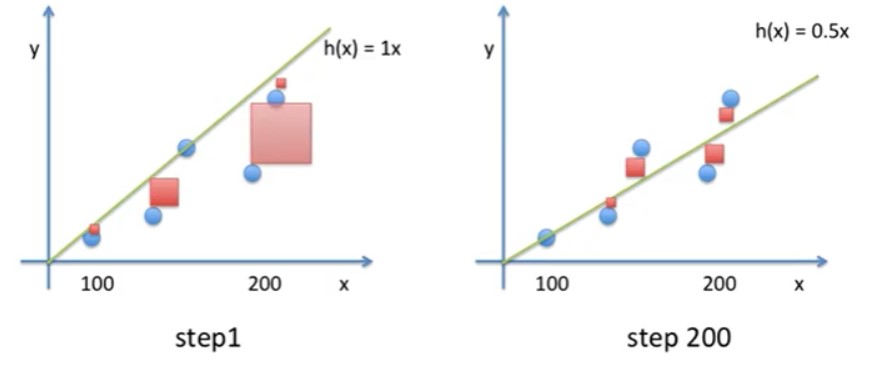
손실을 구한 후 제곱을 해 보면 왼쪽의 직선의 정사각형이 더 작다는 걸 볼 수 있습니다. 그러므로 왼쪽의 직선 모델이 예측을 더 잘할 것입니다.

---

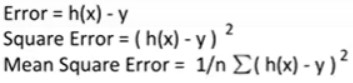
3. 경사하강법(Gradient Descent)

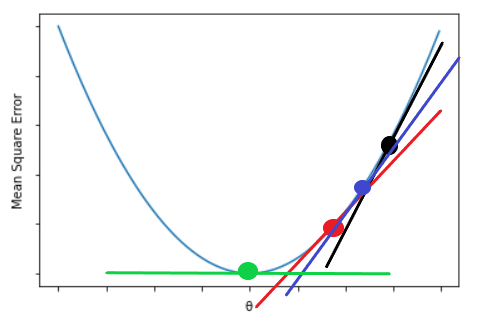
어떻게 하면 손실을 최소화할지 생각해 봅시다. 최적의 선형회귀 모델을 만든 후에 그 모델의 Mean Square Error(=Cost function)을 최소로 만드는 최적의 직선을 찾아야 합니다. cost를 최소화하는 직선을 만드는 과정을 머신 러닝에서 훈련(training) 또는 학습(learning)이라고 부르고 사용되는 알고리즘이 경사 하강법(Gradient Descent) 알고리즘입니다.
손실을 함수로 나타내면 아래와 같습니다. 우리는 기울기인 θ를 최소로 하는 것이 목적입니다

. 첫번째 θ를 1로 주고 α를 0.01로 주겠습니다. α는 learning rate로 학습 속도를 조절하는 상수입니다. 그 후에 θ를 변화시켜 계속하여 converge가 될 때까지 구합니다. converge가 된다는 소리는 θ가 0이 될 때까지를 말합니다.

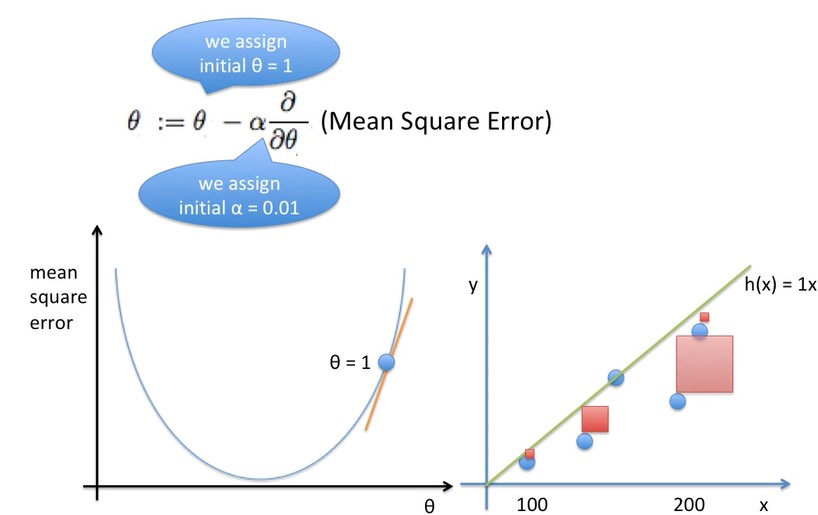
200번을 반복하면 에러가 상당히 줄어든걸 확인해볼 수 있습니다.

4. 수렴

이제 우리는 Learning Rate(α)를 어떻게 설정을 해야되는지 알아보겠습니다. Learning Rate는 θ가 변하는 양을 상수로서 앞에 붙어서 조절합니다.

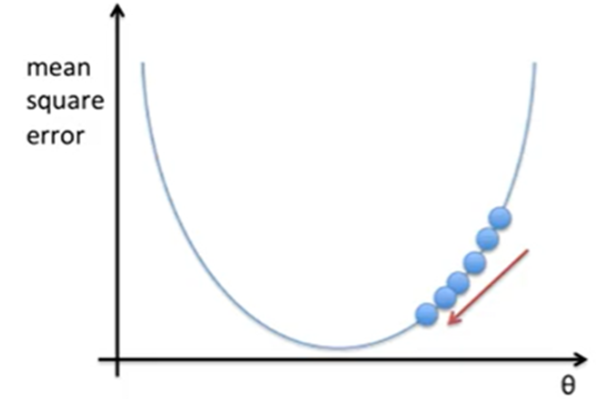
4 - 1. Learning Rate가 낮을 경우

Learning Rate가 낮으면 시간이 오래걸립니다. 그러면 converge를 찾는 과정이 오래 걸리기 때문에 효율적이지 못합니다.

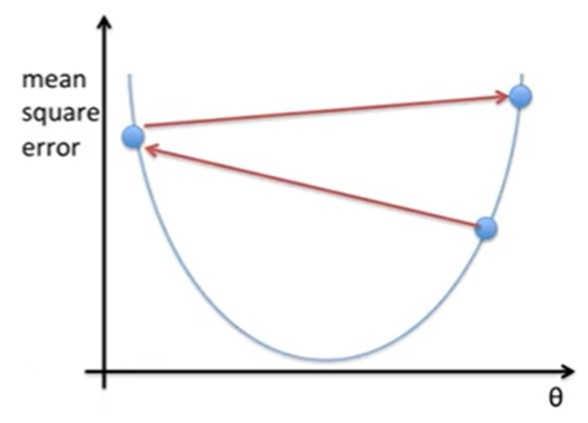
4 - 2. Learning Rate가 높을 경우

그렇다고 Learning Rate(α)가 높으면 안좋은 결과를 초래합니다. Learning Rate(α)가 높기 때문에 최저점을 수렴하지 않고 converge를 지나칠 수 있습니다.

Learning Rate(α)를 적절히 조정하다보면 어떠한 특이점에서 결과값이 수렴하는 것을 볼 수 있습니다.